File:FS HC dia.png
FS_HC_dia.png (680 × 425 pixels, file size: 20 KB, MIME type: image/png)
Captions
Captions
Summary[edit]
| DescriptionFS HC dia.png |
English: Largest circle in a semicircle
Deutsch: Größter Kreis in einem Halbkreis |
| Date | |
| Source | Own work |
| Author | Hans G. Oberlack |
Licensing[edit]
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

The semicircle as base element. And the largest inscribed circle.
General case[edit]
Segments in the general case[edit]
0) The radius of the semicircle:
1) The radius of the inscribed circle:
Perimeters in the general case[edit]
0) Perimeter of base semicircle: 
1) Perimeter of inscribed circle: 
Areas in the general case[edit]
0) Area of the base semicircle
1) Area of the inscribed circle
Centroids in the general case[edit]
0) By definition the centroid point of a base shape is
1) The centroid of the inscribed circle relative to the base centroid is: 
Normalised case[edit]

In the normalised case the area of the base semicircle is set to 1.
So
Segments in the normalised case[edit]
0) Radius of the base semicircle
1) Radius of the inscribed circle
Perimeter in the normalised case[edit]
0) Perimeter of base semicircle: 
1) Perimeter of inscribed circle: 
S) Sum of perimeters:
Area in the normalised case[edit]
0) Area of the base semicircle is by definition
1) Area of the base semicircle
Centroids in the normalised case[edit]
0)
1) 
Distances of centroids[edit]
The distance between the centroid of the base semicircle and the centroid of the circle is:
Sum of distances:
Identifying number[edit]
Apart of the base element there is only one shape allocated. Therefore the integer part of the identifying number is 1.
The decimal part of the identifying number is the decimal part of the sum of the perimeters and the distances of the centroids in the normalised case.
So the identifying number is: 
Calculations[edit]
Calculation 1[edit]
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 22:01, 21 May 2022 |  | 680 × 425 (20 KB) | Hans G. Oberlack (talk | contribs) | new version |
| 16:51, 21 May 2022 | 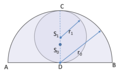 | 680 × 425 (22 KB) | Hans G. Oberlack (talk | contribs) | Uploaded own work with UploadWizard |
You cannot overwrite this file.
File usage on Commons
The following 2 pages use this file:
Metadata
This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.
| Horizontal resolution | 59.06 dpc |
|---|---|
| Vertical resolution | 59.06 dpc |
| Software used |




















